CPC2020决赛赛题公布

各参赛队，CPC2020决赛赛题公布如下：

决赛赛题：基于非结构网格的通用计算加速算法

上机平台：神威·太湖之光

赛题背景

非结构网格由于具有较好的几何适应性，在科学计算中占据了越来越重要的地位。但是基于非结构网格的高可信度应用仍然非常耗时，高精度的湍流模型会带来极大的计算开销，不得不借助于超级计算机来实现大规模并行来提高求解效率。

但是非结构网格引入的离散访存特性使得开发人员需要结合硬件特性和并行模型对求解程序进行精细的调试才能实现较高的并行效率，这种多领域合作对高性能工程师和科学计算工程师都提出了较高的挑战；另一方面，超级计算机芯片的种类繁多，同种芯片的更新换代频率也很高，因此为了兼容性和与时俱进，科学计算软件可能也需要开发出不同版本并随着软硬件的更新换代而不断迭代，这极大的增加了科学计算软件高性能化的难度。

因此本次比赛希望开发一种基于非结构网格的通用计算加速算法，屏蔽数值算法的众核并行实现细节，使得该并行加速算法可以兼容各种非结构网格遍历计算算子。

赛题简介

非结构网格的遍历计算可分为三部分：数据集、拓扑和算子。数据集即为定义在网格顶点或者边上的各种数据（数组）的集合；拓扑可以理解为网格顶点与边之间的连接关系，通常以稀疏矩阵形式存储；算子即为各种数组算法的具体实现。实际上拓扑的遍历与具体的算子和数据集无关，因此选手需要实现一种基于给定的拓扑进行高效遍历的算法，该算法支持各种给定计算模式下的算子及相应的数据集。

本次比赛的算子计算模式限制为以下三种：

1.顶点状态的更新

2.边状态的更新

3.通过邻居顶点及边状态更新点状态

以上三种模式的共同特点在于状态信息在顶点与边之间进行流动传播，且可将边视为基本单元，顶点为连接单元，计算过程可以总结为遍历非结构网格所有的边，获取每条边上的左右顶点的状态，与自身边状态进行运算，最终用计算结果更新左右顶点的状态或者自身状态：

比赛中所用测试算子在满足以上三种计算模式下会有以下几种不确定性：

1.状态间的运算不确定，包括加减乘除以及标准C中的数学库函数；

2.节点或边的状态数目不确定，即节点或边可能有多个状态参与运算，在稀疏矩阵向量乘法中，顶点的状态个数为2，边的状态个数为1，其它测试函数中可能更多；

3.节点或边的状态可能为结构体数组(Array-of-Structs)或者二维数组，即某个节点或边上的状态可能为一个结构体或数组，例如某个测试算子中需要顶点的坐标信息，则每个顶点的状态均为维度为3的数组（三维计算），如下图所示。考虑到并行效率，在本次比赛的数据结构中，所有的状态将被存储为标记了结构体维度信息的一维数组。

程序接口

本次比赛选手需要根据官方提供的数据结构及算子设计众核加速算法，直接接口如下所示：

void slave_computation(DataSet *dataSet_edge, DataSet *dataSet_vertex,

    label *row, label *col, FunPtr funPtr)

{

    SlavePara para = {

        row,

        col,

        dataSet_edge,

        dataSet_vertex,

        

        funPtr

    };

    __real_athread_spawn((void*)slave_computation_kernel, &para);

    athread_join();

}

输入参数由官方提供，包括两个稀疏矩阵数组、两个数据集、一个测试函数指针（回调函数）。

该稀疏邻接矩阵可以CSR、COO等形式存储，这两种存储形式广泛应用于科学计算领域，但是在上述存储模式下，图中的边会存储两次，遍历两次，增加了寻址开销，不利于性能调优，考虑到该矩阵为对称矩阵，因此只存储该邻接矩阵的上三角部分，先逐行再逐列存储每条边的行列坐标，即每条边的左右顶点，则稀疏矩阵可以下表形式表示：

需要注意的是，该稀疏矩阵的对称性只局限于拓扑层面，矩阵上非零元素的值不一定对称，即非结构网格上边的值可能是“有方向的”，同样以稀疏矩阵向量乘法Ax=b为例，这里的矩阵A将拆分为上三角和下三角两部分，分别储存于upper和lower数组中，计算时对于某个非零元素，将同时计算上三角和下三角两个位置的值：

    int i;

    for (i = 0; i < n_edge; ++i)

    {

        b[col[i]] += A[i]*x[row[i]];

        b[row[i]] += A[i]*x[col[i]];

    }

2.两个数据集存储边状态及顶点状态信息，存储方式为SoAoS(Struct-of-Arrays-of-Structs)，即SoA和AoS的组合，第一个S指边或者顶点上所存储的状态的集合，A指某一状态下的所有单元状态，第二个S指某一状态下的某一单元的状态值，该值既可能为标量，也可能为向量或者张量，因此以结构体形式存储。输入参数dataSet_edge和dataSet_vertex分别存储边状态集和点状态集。

以稀疏矩阵向量乘b=Ax为例，正如前面提到的，矩阵A将拆分为lower和upper两部分数组，lower和upper为定义在边上的状态集，b和x为定义在点上的状态集，则点状态集的集合存储结构具体如下图所示：

注意，对于某一状态，其虽然以AoS结构存储，但考虑到并行效率，其在内存空间上连续存储，选手可通过结构体维度分段索引。

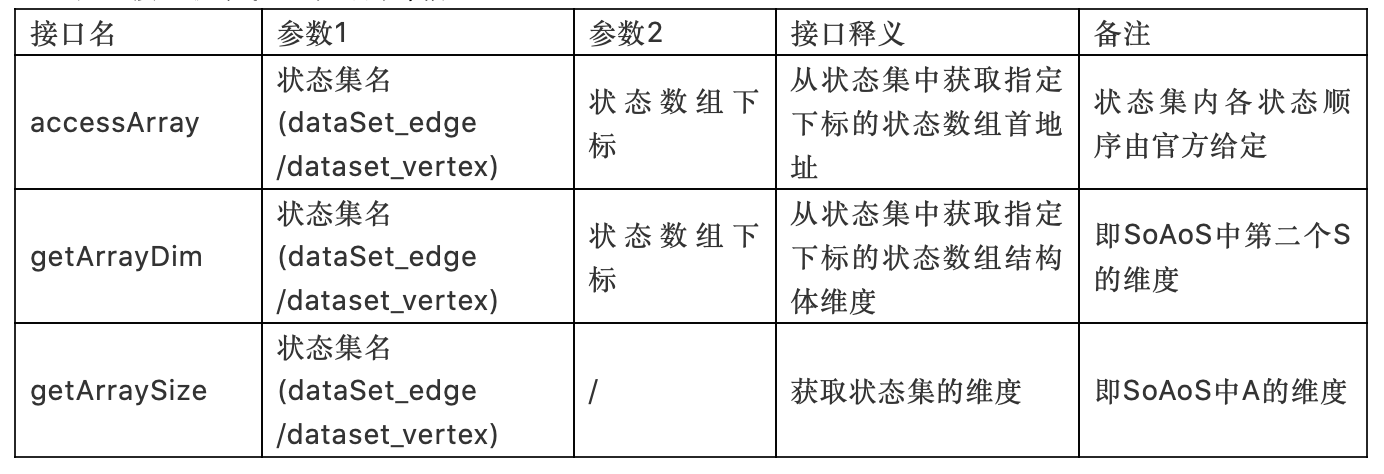
通过以下接口获取状态集的内部信息：

3.函数指针（回调函数）

函数指针定义了状态之间的具体计算操作，选手可对拓扑或者状态集进行重排或预处理，在从核内进行数据分段，然后通过回调函数进行计算。该回调函数的参数列表如下所示：

typedef void (* FunPtr)(DataSet *dataSet_edge, DataSet *dataSet_vertex, label *row, label *col);

代码架构

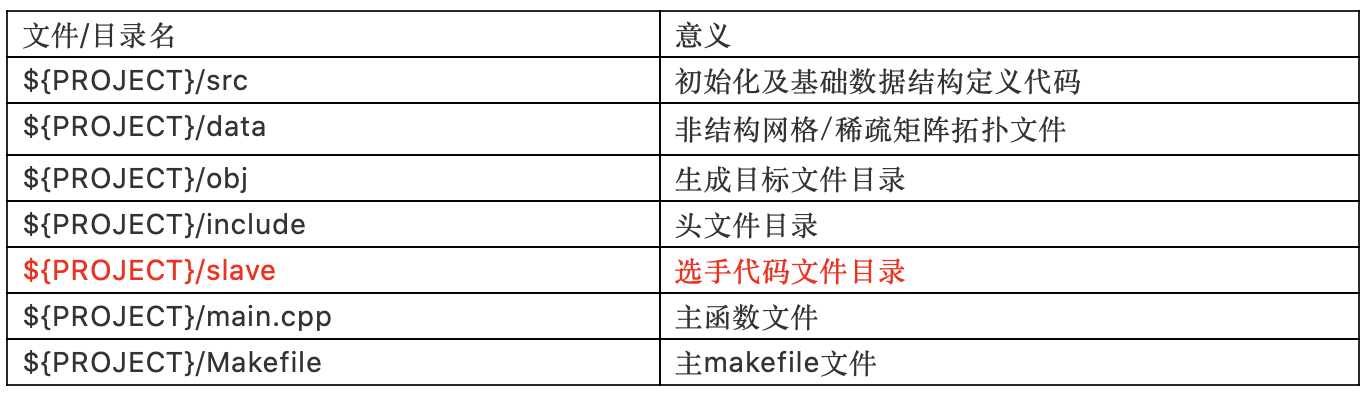
选手只能在slave目录下进行代码编写工作，该目录下已有Makefile样例文件，选手可进行修改，最终将生成的目标文件存储到obj目录下，不可对其他目录下文件进行更改。

赛事规则

1.评分规则

1)  比赛将使用组委会提供的不少于五套测试算例进行评分，每套测试算例由若干组子算例组成；所有子算例具有相同的测试函数，以及不同的稀疏矩阵；对于每个子算例，程序将运行500次，统计从核接口函数slave_computation的平均运行时间；每套算例的运行时间将以各子算例的加权平均结果计算；按照所有测试算例的总运行时间进行排名。

2)  选手必须保证计算结果的正确性，本次比赛采用绝对误差与相对误差对浮点数正确性进行判断，误差限为10的负14方，任意一组测试函数计算结果错误，本次提交成绩无效； 选手可对拓扑（矩阵）以及输入数据进行重排或预处理，但是输出计算结果时需要按照原拓扑进行输出。

3)  选手成绩取个人多次提交里面的最好成绩。

4)  如果时间一样，先提交的选手排名靠前。

2.编译选项

编译链接选项位于Makefile文件中，不得更改。

3.提交选项

bsub –I –b –q q_sw_share –share_size 4096 –host_stack 1024 –n 1 –cgsp 64 <二进制文件>

参考文献

Mudalige, G. R., et al. "Op2: An active library framework for solving unstructured mesh-based applications on multi-core and many-core architectures." 2012 Innovative Parallel Computing (InPar). IEEE, 2012.

赛题及比赛平台由国家超级计算无锡中心提供。